REICE. Revista Iberoamericana sobre Calidad, Eficacia y Cambio en Educación

INTRODUCCIÓN

La resolución de problemas constituye una actividad de aprendizaje ampliamente utilizada en la enseñanza de las ciencias y de las matemáticas. Son múltiples los factores que influyen en la resolución de problemas (Solaz-Portolés y Sanjosé, 2008). Así, por ejemplo, en el trabajo de Orrantia, Múñez y Matilla (2012) se ponen en evidencia las dificultades que tienen los estudiantes para aplicar el conocimiento conceptual en la resolución de problemas.

De acuerdo con Mayer (1992), para poder resolver un problema es necesario construir una representación mental adecuada a partir de su enunciado. Para elaborar esta representación mental el sujeto solucionador tiene que efectuar, según el autor, dos pasos: la traducción y la integración del problema. En la traducción el sujeto ha de extraer los conceptos del enunciado mediante su conocimiento lingüístico y semántico. El primero se utiliza para comprender el significado de las palabras, mientras que el segundo se emplea para comprender la situación que el problema plantea. En la integración del problema el sujeto ha de construir proposiciones y interconectarlas a partir de la información proporcionada en el enunciado; a continuación, y haciendo uso de sus conocimientos previos, les da una estructura coherente en forma de representación mental o modelo mental. Cuando la información del enunciado del problema se ha transformado en un modelo mental adecuado se puede afirmar que el sujeto ha comprendido el problema y está en condiciones de abordar su resolución.

Los problemas de aplicación realista o auténticos problemas son aquellos que reproducen situaciones del mundo real (Vicente y Orrantia, 2007). Para estos problemas, que son una parte de los que se llevan a cabo en el aula de ciencias (en física y química sobre todo), Verschaffel, Greer y De Corte (2000) proponen un modelo de resolución de problemas según el cual, para resolver problema, el sujeto, primero, ha de comprender la situación descrita por el problema y elaborar un modelo de la situación del mismo; y a partir de él, debe construir un modelo matemático que recoja los elementos esenciales de esa situación problemática y de las relaciones existentes entre ellos (esto es, la estructura del problema), para luego extraer las implicaciones que se derivan de ese modelo matemático para resolver el problema e interpretar los resultados obtenidos.

Nosotros estamos particularmente interesados en cómo la utilización de símbolos junto a los enunciados de los problemas de ciencias físicas puede influir en los procesos de resolución. Este interés se debe al hecho de que, en los últimos años, varias editoriales han incluido dichos símbolos en los libros de texto de la E.S.O.

1. FUNDAMENTACIÓN TEÓRICA

La construcción de un modelo mental adecuado para resolver un problema va a depender, por un lado, de la disponibilidad de una amplia gama de conocimientos y estrategias (Solaz-Portolés y Sanjosé, 2007) y, por otro, de la capacidad de reconocer que la estructura del problema que tenemos que resolver es similar a la de otros que hemos resuelto previamente (Gómez, Sanjosé y Solaz-Portolés, 2012). Por esta razón, será necesario que se pueda acceder a la estructura del problema y que se disponga de los conocimientos de esquemas de problema apropiados (esto es, haber resuelto previamente problemas de estructura similar al que intenta resolver).

No obstante, en los procesos de elaboración de un modelo mental apropiado del problema a resolver está implicada no sólo la capacidad de análisis de la información que aparece en el enunciado, sino también la autoevaluación que la persona hace de su conocimiento de la tarea, del nivel de dificultad y de las posibilidades de éxito (Garofalo y Lester, 1985).

De acuerdo con O’Malley y Chamot (1990) las estrategias cognitivas son herramientas que ayudan al estudiante a recoger, relacionar y recordar información, y que requieren de la interacción con los materiales didácticos, que se han de manipular física o mentalmente. Estos autores definen las estrategias metacognitivas como habilidades de alto nivel que posibilitan la planificación, el control y la evaluación de los procesos a llevar a cabo durante una actividad de aprendizaje. Varios investigadores han concluido que las destrezas metacognitivas mejoran con la edad (Kuhn y Dean, 2004; Schneider, 2008; Schraw y Moshman, 1995). Además, aparece en la literatura que las estrategias cognitivas y metacognitivas están muy relacionadas, llegándose a afirmar que las estrategias metacognitivas tienen un impacto directo sobre las cognitivas (Anderson, 2005; Chamot, 2005; Wenden, 1991).

Solaz-Portolés, Sanjosé y Gangoso (2013) han puesto de relieve el destacado papel que desempeñan las destrezas metacognitivas en la resolución de problemas, que permiten a los estudiantes exitosos en esta tarea seleccionar los planes más adecuados durante la resolución del problema, superar los posible obstáculos y evaluar de forma constante su progreso hacia la solución.

Como consecuencia de todo lo dicho, es razonable pensar que la posible influencia de símbolos junto al enunciado de un problema sobre los procesos de resolución, dependerá en gran medida de las estrategias cognitivas y metacognitivas del potencial solucionador. Además, es ineluctable que dichos símbolos también pueden alterar, antes del inicio de la lectura del enunciado del problema, la motivación con la que el estudiante se va a enfrentar a la tarea. Hay trabajos que han puesto en evidencia la correlación existente entre factores motivacionales y el éxito en la resolución de problemas (Coutinho, Wiemer-Hastings, Skowronski y Britt, 2005; Marcou y Philippou, 2005). Por otro lado, ha sido ampliamente estudiada la repercusión de las actitudes y expectativas del alumno en el desempeño en la resolución de problemas (Greeno, 1991; Jonassen, 2000; Mayer, 1998).

2. OBJETIVO DEL ESTUDIO E HIPÓTESIS

El objetivo del presente trabajo es estudiar los efectos, en estudiantes de secundaria, del uso de símbolos que indiquen el nivel de dificultad junto al enunciado de los problemas sobre el rendimiento en su resolución, y el papel que desempeña en dichos efectos el nivel académico de los estudiantes.

Basándonos en todo el bagaje teórico expuesto anteriormente nuestras hipótesis son que:

• Existirán diferencias significativas en las calificaciones obtenidas por los estudiantes al resolver problemas, en función del símbolo de nivel de dificultad que se encuentre junto al enunciado del problema. Esto es, un mismo problema señalizado con un símbolo distinto de nivel de dificultad será resuelto con distinto éxito.
• El nivel académico intervendrá de manera decisiva en los efectos del símbolo de nivel de dificultad junto al enunciado: los estudiantes de mayor nivel académico se verán poco influidos por el símbolo. Es decir, los estudiantes de mayor nivel académico resolverán con igual desempeño un determinado problema independientemente de la señalización de su nivel de dificultad.

3. METODOLOGÍA

3.1. Diseño experimental

Se siguió una metodología mixta en dos fases: en la primera se lleva a cabo un análisis cuantitativo (descriptivo y con los contrastes pertinentes) y en la segunda un análisis cualitativo (entrevistas semi-estructuradas). En la primera fase, se utilizó un diseño factorial con dos variables entre-sujetos, señalización del problema (con dos valores, real –o directa- e inversa) y nivel académico (con dos valores, 4º de ESO y 2º de Bachillerato); y una variable intra-sujetos, tipo de problema (con dos valores, fácil o difícil). La calificación obtenida por los estudiantes en los problemas se tomó como variable dependiente.

3.2. Selección de los problemas del estudio cuantitativo

3.2.1. Sujetos participantes

Participaron 27 estudiantes de dos grupos (de 12 y 15 alumnos) de primero de Bachillerato que cursaban la asignatura de Física y Química. Dichos grupos pertenecían a dos institutos de educación secundaria (IES) públicos de la ciudad de Valencia. No existe ningún aspecto que indique que estos alumnos difieran del común de los alumnos de 1º de bachillerato de Física y Química, sin embargo, no puede hablarse de un muestreo estadístico pues se trabajó con grupos completos, configurando una muestra de conveniencia.

3.2.2. Materiales

Se elaboraron cuadernillos que contenían dos problemas de móviles de similar estructura (de un conjunto de 6 problemas –Anexo I- que habíamos preparado y que se diferencian bien en la posición de inicio de los móviles, bien en el instante de inicio del movimiento): dos móviles con movimiento rectilíneo uniforme (MRU) y que uno alcanza al otro. En los cuadernillos no había ninguna indicación sobre su dificultad, y se les informaba que podían comenzar por el que quisieran y distribuir el tiempo disponible (40 minutos) a su antojo. Se escogieron estos problemas porque los conocimientos matemáticos y físicos necesarios para su resolución se imparten por completo en 4º de ESO. Son problemas del mismo tipo que los que aparecen en la mayoría de libros de texto, por lo que, en realidad, no son “auténticos problemas” (Schoenfeld, 1992).

3.2.3. Procedimiento

Se distribuyeron al azar tres tipos de cuadernillos diferentes cada uno de ellos con dos problemas. Los cuadernillos se recogieron a los 40 minutos del inicio del ejercicio y fueron calificados por dos profesores (uno de secundaria y uno de la universidad) de acuerdo con protocolo establecido por dos profesores universitarios, que puede hallarse en el Anexo II. El acuerdo interjueces fue superior al 95% y se resolvieron las discrepancias de mutuo acuerdo. Tras obtener las puntuaciones de todos los problemas de los cuadernillos, se seleccionaron los dos más parecidos entre sí entre los que obtuvieron la calificación media más baja (problema difícil) y más alta (problema fácil). Estos problemas son los que se han utilizado en el estudio cuantitativo.

3.3. Estudio cuantitativo

3.3.1. Sujetos participantes

Participaron 34 estudiantes de 4º ESO, que cursaban la asignatura de Física y Química, y 33 estudiantes de 2º de Bachillerato, que cursaban la asignatura de Física. Los estudiantes de 4º ESO pertenecen a dos centros de la ciudad de Valencia; los de 2º de Bachillerato a cuatro centros, tres de la ciudad de Valencia y uno de una comarca próxima. Todos los estudiantes de las muestras pertenecían a grupos naturales en sus centros educativos. Se trató de muestras de conveniencia a las que se tuvo acceso tras obtener los permisos pertinentes. Por tanto, la validez externa no está garantizada. A pesar de ello, los centros educativos participantes no poseen ninguna característica particular que los distinga de otros situados en ciudades de cierto tamaño, y los estudiantes no sufrieron selección alguna para ser asignados a los grupos naturales.

3.3.2. Materiales

Se diseñaron dos modelos de cuadernillo, que contenían los enunciados de los problemas seleccionados en la primera fase (recordemos que son problemas de cinemática de estructura “móvil en movimiento rectilíneo y uniforme que alcanza a otro móvil también en movimiento rectilíneo y uniforme” que han resultado ser de diferente dificultad) marcados de diferente modo: uno con un semáforo verde y la palabra fácil, y el otro con un semáforo en rojo y la palabra difícil. Así pues, la única diferencia entre ambos cuadernillos es la asignación de uno u otro semáforo (en verde o en rojo) a cada problema, con su correspondiente grado de dificultad (fácil o difícil). Pueden verse en el Anexo III dichos cuadernillos.

Por el carácter prospectivo del estudio, se optó por utilizar un diseño fragmentado. Esto supone que hemos empleado exclusivamente cuadernillos en los que en uno de los enunciados de los problemas se utilizaba el símbolo “fácil” y, en el otro el símbolo “difícil”. En una versión ampliada o réplica del estudio deberían incluirse dos nuevos modelos de cuadernillo con los enunciados de los dos problemas señalizados del mismo modo (“fácil”-“fácil” y “difícil”-“difícil”).

3.3.3. Procedimiento

Se solicitó a los centros participantes el uso de una sesión de clase completa para que los estudiantes tuvieran tiempo de resolver los dos problemas del cuadernillo. En todos los grupos naturales se distribuyeron al azar los dos modelos de cuadernillos. Mientras los materiales se repartían al azar entre los alumnos, se les indicó que disponían de un tiempo de cuarenta minutos. Un porcentaje superior al 80% de los alumnos entregó el cuadernillo antes del tiempo límite fijado.

Los problemas resueltos por los alumnos fueron calificados según el protocolo mencionado anteriormente (Anexo II). Cada problema recibía una puntuación entre 0 y 1. Los problemas fueron evaluados por los un profesor de secundaria y uno de la universidad, obteniendo un acuerdo interjueces superior al 96 %, y resolviendo las discrepancias de mutuo acuerdo.

3.4. Estudio cualitativo

3.4.1. Sujetos participantes

Entrevistamos a dos estudiantes de 2º de Bachillerato y dos de 4º de la ESO. En ambos niveles académicos uno de los estudiantes se seleccionó porque obtuvo una puntuación acorde con la dificultad real de los problemas y no de la señalización de los mismos, y el otro porque puntuó de la manera contraria. Se buscaron en ambos niveles los dos casos más extremos, esto es, que la diferencia de las puntuaciones entre ambos problemas fuera la máxima.

3.4.2. Procedimiento

Las entrevistas, realizadas con los permisos pertinentes de la dirección de los centros, se realizaron una semana después de la tarea de resolución de los problemas, de modo individual, y en un espacio del centro educativo con privacidad. Las entrevistas fueron grabadas para ser posteriormente transcritas y analizadas. Se llevó a cabo un procedimiento semi-estructurado consistente en:

• Mostrar el cuadernillo con los problemas resueltos por el estudiante.
• Preguntar en qué modo había influido la señalización del problema para abordar la resolución de cada uno de los dos problemas
• Solicitar opinión al estudiante acerca de cómo habría actuado ante el caso de que los problemas no hubieran sido señalizados
• Demandar la lectura atenta y reflexiva de los enunciados de los problemas y pedir el parecer sobre la corrección de la señalización de los problemas.

No se limitó el tiempo de la entrevista y en ningún caso se emitió juicio alguno sobre las respuestas u opiniones expresadas por los estudiantes.

4. RESULTADOS Y DISCUSIÓN

En la tabla 1 se recogen las puntuaciones medias obtenidas (con sus correspondientes desviaciones típicas) en cada tipo de problema (problema fácil y problema difícil), según en el modelo de cuadernillo (modelo 1, de señalización directa o real –el problema fácil marcado como fácil y el problema difícil como difícil-; y modelo 2, de señalización inversa –el problema fácil marcado como difícil y el problema difícil como fácil), y el nivel académico de los estudiantes. También aparece en dicha tabla el número de sujetos (N) que resolvió cada tipo de problema.

Con la finalidad de hacer más visibles las diferencias de las puntuaciones de los problemas en función del nivel académico y de los símbolos utilizados junto al enunciado (es decir, del modelo de cuadernillo empleado), se han representado gráficamente dichas puntuaciones en las figuras 1 (para el caso del cuadernillo con señalización directa o real de los problemas) y 2 (para el caso del cuadernillo con señalización inversa de los problemas).

Tabla 1. Puntuaciones medias en los problemas (con su correspondiente desviación típica y número de sujetos N) según el modelo de cuadernillo y nivel académico

Fuente: Elaboración propia.

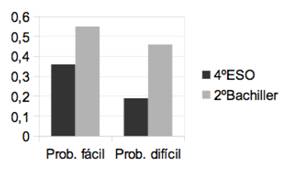
Figura 1. Puntuaciones obtenidas por los estudiantes de 4º de ESO y 2º de Bachillerato en el problema fácil y en el difícil en el modelo de cuadernillo de señalización directa (Modelo 1)

Fuente: Elaboración propia.

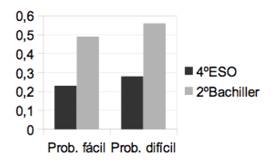
Figura 2. Puntuaciones obtenidas por los estudiantes de 4º de ESO y 2º de Bachillerato en el problema fácil y en el difícil en el modelo de cuadernillo de señalización inversa (Modelo 2)

Fuente: Elaboración propia.

Para poner a prueba nuestras hipótesis, llevamos a cabo un ANOVA tomando el tipo de problema (dos valores, fácil y difícil) como variable intra-sujetos; y el modelo de cuadernillo (dos valores, señalización directa e inversa) y el nivel académico (dos valores, 4º de ESO y 2º de Bachillerato), como variables inter-sujetos. Las puntuaciones obtenidas en los problemas fueron la variable dependiente.

El ANOVA pone de manifiesto que las variables tipo de problema y modelo de cuadernillo no resultan ser significativas en la puntuación de los problemas. Sin embargo, la variable nivel académico sí produce diferencias significativas en la puntuación de los problemas, F(1,63)= 10,81, p<0,01; de modo que los estudiantes de 2º de Bachillerato obtienen puntuaciones significativamente más altas en los problemas que los de 4º de la ESO. Además, y esto es lo más importante, se observa en el análisis que la interacción entre las variables tipo de problema y modelo de cuadernillo genera diferencias estadísticamente significativas en un nivel de confianza superior al 95 %, F(1,63)=5,67, p<0,05. Las restantes interacciones no son significativas. Esta interacción significativa entre ambas variables puede visualizarse en la figura 3. En esta figura se aprecian claramente las diferentes puntuaciones del problema fácil y difícil según aparezcan marcados como fáciles o difíciles en los correspondientes modelos de cuadernillo. Así, se observa que el problema fácil, cuando se señaliza como difícil, genera puntuaciones más bajas que el difícil, situación que se invierte en el caso del problema difícil.

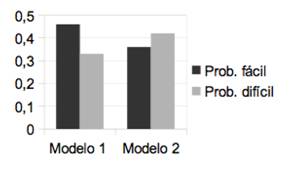
Figura 3. Puntuaciones en el problema fácil y difícil según el modelo de cuadernillo en el que figuran, Modelo 1 (señalización real o directa) o Modelo 2 (señalización inversa)

Fuente: Elaboración propia.

La tabla 2 muestra fragmentos de las entrevistas realizadas a los estudiantes de 2º de Bachillerato. También ofrece también fragmentos de las entrevistas, en este caso de los estudiantes de 4º de ESO.

A partir de estos fragmentos de entrevistas pueden entreverse dónde se focalizan principalmente los efectos de la señalización de los problemas. Se destaca que solamente al estudiante del caso #1, que pone de manifiesto una elevada autoeficacia y buenas estrategias de resolución de problemas (fijémonos en el detalle que ha evaluado el nivel de dificultad del problema que estaba marcado como fácil diciendo que le costó resolverlo), es capaz de tener sospechas de que el marcado de dificultad puede ser incorrecto. Además, en este estudiante el símbolo sólo parece orientarle hacia el orden de resolución de los problemas, no en el potencial esfuerzo que debe hacer para resolverlo. Es decir, no altera su motivación en la resolución.

Los estudiantes de los casos #2 y #4 representan el polo opuesto. Ambos tienen la percepción de que su autoeficacia en la resolución de problemas es baja y, consecuentemente, se dejan llevar completamente por la señalización de los problemas, que acaba influyéndoles negativamente cuando abordan su resolución, puesto que piensan que si el problema es difícil no lo podrán resolver. Como puede verse, sus estrategias de resolución de problemas son pobres: actúan por “ensayo y error” probando ecuaciones, sin llegar a elaborar, por tanto, una representación mental (o modelo mental) apropiada.

Tabla 2. Fragmentos de las entrevistas de dos estudiantes de 2º de Bachillerato y 4º ESO

Caso #1 (Estudiante con puntuación de acuerdo con la dificultad real de los problemas) (2º Bachillerato) Entrevistador (Ent): Buenos días. ¿Recuerdas la prueba de resolución de dos problemas de la semana pasada? [El entrevistador entrega el cuadernillo de problemas] Estudiante (Est): Sí, eran dos problemas de cinemática distintos, uno fácil y otro más difícil... [El estudiante mira y lee el cuadernillo] Ent: ¿Cómo te influyó el semáforo señalizador de la dificultad de los problemas? Est: Me hizo ir directo a resolver el que se indicaba que era más fácil, aunque me costó bastante resolverlo...después hice el otro sin problemas... Ent: Si no hubiera estado el semáforo, ¿qué habrías hecho? Est: Creo que los hubiera resuelto en el orden en que están...me va bien resolver problemas... Ent: Por favor, vuélvete a leer los enunciados y dime si está bien indicada su dificultad. Est: [El estudiante lee detenidamente ambos, y los vuelve a releer] Me parece que la señalización no es la correcta..., debería ser al revés, pero no acabo de estar seguro...

Caso #2 (Estudiante con puntuación invertida en relación a la dificultad real de los problemas) (2º Bachillerato) Ent: Buenos días. ¿Recuerdas la prueba de resolución de dos problemas de la semana pasada? [El entrevistador entrega el cuadernillo de problemas] Est: Sí, se tenían que hacer dos problemas ... [El estudiante prácticamente ni mira el cuadernillo] Ent: ¿Cómo te influyó el semáforo señalizador de la dificultad de los problemas? Est: Para mí es básico tener este dato. Si un problema es difícil, imposible que lo pueda hacer...lo planteo, pongo las fórmulas, busco las incógnitas, pero pocas veces me salen bien... Ent: Si no hubiera estado el semáforo, ¿qué habrías hecho? Est: ¡Uf!, como en los exámenes. Me leo el problema, si me sé fórmulas y puedo aplicarlas empiezo a resolverlo, hasta que veo claro como despejar lo que me piden... Ent: Por favor, vuélvete a leer los enunciados y dime si está bien indicada su dificultad. Est: [El estudiante lee detenidamente ambos] Sí, está bien.

Caso #3 (Estudiante con puntuación de acuerdo con la dificultad real de los problemas) (4º Eso) Ent: Buenos días. ¿Recuerdas la prueba de resolución de dos problemas de la semana pasada? [El entrevistador entrega el cuadernillo de problemas] Est: Claro, eran problemas de coches y ciclistas... [El estudiante mira el cuadernillo] Ent: ¿Cómo te influyó el semáforo señalizador de la dificultad de los problemas? Est: Me hizo que me esforzara más en encontrar la solución...digamos que igual que los libros, cuando tienen colores más fácil o menos... tienes que concentrarte más.. Ent: Si no hubiera estado el semáforo, ¿qué habrías hecho? Est: Leerlos y ver cuál es mejor para empezar porque veo claro cómo plantearlo, sé las ecuaciones...y creo que lo voy a hacer bien Ent: Por favor, vuélvete a leer los enunciados y dime si está bien indicada su dificultad. Est: [El estudiante lee detenidamente ambos, ocupándole un tiempo considerable] Sí... sí ... no puede estar mal

Caso #4 (Estudiante con puntuación invertida en relación a la dificultad real de los problemas) (4º Eso) Ent: Buenos días. ¿Recuerdas la prueba de resolución de dos problemas de la semana pasada? [El entrevistador entrega el cuadernillo de problemas] Est: Sí, eran problemas de calcular kilómetros ... [El estudiante mira el cuadernillo] Ent: ¿Cómo te influyó el semáforo señalizador de la dificultad de los problemas? Est: Me influyó mucho porque sé que así puedo hacerlo o no... Me cuesta hacer problemas que son difíciles y tengo que pensarlo...Me gusta que me digan que puedo hacerlo... Ent: Si no hubiera estado el semáforo, ¿qué habrías hecho? Est: Probar... Miro a ver cuál es más fácil, porqué así voy a lo seguro...Si me sé las fórmulas, busco enseguida el camino para la solución... Si sale lo que busco, sigo adelante, si no, lo dejo... Ent: Por favor, vuélvete a leer los enunciados y dime si está bien indicada su dificultad. Est: [El estudiante lee detenidamente ambos] Yo creo que sí.

Fuente: Elaboración propia.

En el estudiante del caso #3, la señalización de los problemas hace que se pongan en marcha más recursos cognitivos cuando se trata de un problema marcado como difícil. Por tanto, afecta a su planificación de resolución y autocontrol (estrategias metacognitivas); y a su motivación de manera positiva, ya que le invita a esforzarse más. Además, de lo que dice puede deducirse que lleva a cabo un planteamiento cualitativo previo a la resolución, lo que puede ser una fase de tránsito hacia la elaboración de un modelo mental. Con todo ello, se puede decir que sus estrategias son mejores que las de los estudiantes #2 y #4.

5. CONCLUSIONES

La interacción significativa encontrada entre las variables tipo de problema y modelo de cuadernillo, y reflejada en la figura 3, parece corroborar nuestra primera hipótesis: utilizar símbolos junto al enunciado que señalizan sobre el grado de dificultad de los problemas influye en el rendimiento de su resolución. Así, por ejemplo, si un problema que objetivamente puede considerarse fácil, se marca como difícil, hace disminuir significativamente el rendimiento de los estudiantes de secundaria en su resolución.

Como puede observarse en las figuras 1 y 2, el nivel académico conduce a mejores puntuaciones en los problemas: los estudiantes de 2º de Bachillerato siempre puntúan más alto en los problemas. De hecho, la variable nivel académico ha generado en el análisis de varianza diferencias significativas en la calificación de los problemas. Este resultado es el previsible, atendiendo al mayor conocimiento previo y mejores estrategias de resolución, fruto todo ello de sus dos cursos más de formación que los de 4º de la ESO.

Sin embargo, las interacciones entre la variable nivel académico y las otras dos variables, tipo de problema y modelo de cuadernillo no han resultado ser significativas. Este hecho puede constatarse por comparación de las Figuras 1 y 2. Tanto los estudiantes de 4º de la ESO como los de 2º de Bachillerato se ven afectados por la señalización de los problemas. En consecuencia, la variable nivel académico no altera significativamente el efecto del uso del símbolo para señalizar el nivel de dificultad de los problemas. Así, nuestra segunda hipótesis, que defendía precisamente lo contrario, queda invalidada. Probablemente, hemos sobrevalorado las estrategias cognitivas y metacognitivas que podrían utilizar los estudiantes de 2º de Bachillerato para no dejarse influenciar por el marcado del grado de dificultad de los mismos.

Las entrevistas efectuadas permiten proporcionar indicios de los efectos de la señalización de los problemas en relación a los perfiles cognitivos de los estudiantes. Así, se destaca que cuando se tiene una elevada autoeficacia y buenas estrategias de resolución de problemas, los símbolos junto a los problemas prácticamente no afectan a los procesos de resolución. Sin embargo, en el extremo opuesto, con una baja autoeficacia y pobres estrategias de resolución, el símbolo en un problema que indica que es difícil desmotiva completamente al estudiante, que reduce sus expectativas de éxito y su nivel de esfuerzo ante la resolución. Finalmente, en el caso de no estar en los extremos anteriores, nos encontramos que la señalización incluso puede llegar a tener consecuencias positivas: pone en alerta estrategias metacognitivas (planificación y autocontrol) e incrementa la motivación (aumenta el esfuerzo durante la resolución).

Las consecuencias que pueden derivarse de este trabajo, con la prudencia que exigen las limitaciones del mismo (muestra reducida, diseño fragmentado, un único tipo de problemas –cinemática y de la misma estructura-, etc), deben hacer referencia a los efectos didácticamente negativos que pueden confluir en la asignación de la dificultad en los enunciados de los problemas: llegan a afectar y desmotivar a una buena parte de los estudiantes de secundaria en sus procesos de resolución. Esperemos que la editoriales tomen buena nota de los peligros derivados de esta práctica.

REFERENCIAS

Anderson, N.J. (2005). L2 learning strategies. En E. Hinkel (Ed.), Handbook of research in second language teaching and learning (pp. 757–771). Mahwah, NJ: Lawrence Erlbaum.

Chamot, A.U. (2005). Language learning strategy instruction: Current issues and research. Annual Review of Applied Linguistics, 25, 112-130.

Coutinho, S.A., Wiemer-Hastings, K., Skowronski, J.J. y Britt, M.A. (2005). Metacognition, need for cognition and use of explanations during ongoing learning and problem solving. Learning and Individual Differences, 15, 321-337.

Garofalo, J. y Lester, F. (1985). Metacognition, cognitive monitoring, and mathematical performance. Journal of Research in Mathematics Education, 16(3), 163-176.

Gómez, C.B., Sanjosé, V. y Solaz-Portolés, J.J. (2012). Una revisión de los procesos de transferencia para el aprendizaje y enseñanza de las ciencias. Didáctica de las Ciencias Experimentales y Sociales, 26, 199-227.

Greeno, J. (1991). A view of mathematical problem solving in school. En M.U. Smith (Ed.), Toward a unified theory of problem solving (pp. 69-98). Hillsdale, NJ: Lawrence Erlbaum Associates.

Jonassen, D. (2000). Toward a design theory of problem-solving. Educational Technology: Research and Development, 48, 63 - 85.

Kuhn, D. y Dean, D. (2004). A bridge between cognitive psychology and educational practice. Theory into Practice, 43(4), 268-273.

Marcou, A. y Philippou, G. (2005) Motivational beliefs, self-regulated learning and mathematical problem solving. En H.L. Chick y J.L. Vincent (Eds.), Proceedings of the 29 Conference of the International Group for the Psychology of Mathematics Education (pp. 297-304). Melbourne: PME

Mayer, R.E. (1992). Thinking, problem solving and cognition. Nueva York: Freeman.

Mayer, R.E. (1998). Cognitive, metacognitive, and motivational aspects of problem solving. Instructional Science, 26, 49 – 63

O’Malley, J.M. y Chamot, A.U. (1990). Language Strategies in Second Language Acquisition. Cambridge: Cambridge University Press.

Orrantia, J., Múñez, D., Fernández, M. y Matilla, L. (2012). Resolución de problemas aritméticos: Conocimiento conceptual y nivel de competencia en matemáticas. Aula Abierta, 40(3), 23-32.

Schneider, W. (2008). The development of metacognitive knowledge in children and adolescents: Major trends and implications for education. Mind, Brain, and Education, 2(3), 114-121.

Schoenfeld, A.H. (1992). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics. En D. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 334-370). Nueva York: McMillan.

Schraw, G. y Moshman, D. (1995). Metacognitive theories. Educational Psychology Review, 7(4), 351-371.

Solaz-Portolés, J.J. y Sanjosé, V. (2007). Representations in problem solving in science: Directions for practice. Asia Pacific Forum on Science Learning and Teaching, 8(2), art. 8.

Solaz-Portolés, J.J. y Sanjosé, V (2008). Conocimientos y procesos cognitivos en la resolución de problemas de ciencias: consecuencias para la enseñanza. Magis, Revista Internacional de Investigación en Educación, 1, 147-162.

Solaz-Portolés, J.J., Sanjosé, V. y Gangoso, Z. (2013). La investigación en resolución de problemas instruccionales. Efectos de variables del problema y de las variables cognitivas, metacognitivas y motivacionales del resolutor. En J. Benegas, M.C. Pérez de Landazábal y J. Otero (Eds.), El aprendizaje activo de la Física Básica Universitaria (pp. 95-118). Santiago de Compostela: Andavira Editora.

Verschaffel, L., Greer, B. y De Corte, E. (2000). Making sense of word problems. Lisse: Swets & Zeitlinger Publishers.

Vicente, S. y Orrantia, J. (2007). Resolución de problemas y comprensión situacional. Cultura y Educación, 19, 61-85.

Wenden, A.L. (1991). Learner strategies for learner autonomy. Englewood Cliffs, NJ: Prentice-Hall.

--------------

ANEXO I: ENUNCIADOS PARA LA SELECCIÓN DE LOS PROBLEMAS

Problemas de dos móviles con tiempo inicial diferente

Problema 1

Dos coches salen del mismo punto para realizar un trayecto por una carretera recta. El primero sale a las 12:00 con una velocidad de 100 km/h y el segundo sale a las 12:30 con una velocidad de 120 km/h.¿A qué distancia del punto de origen se encontrarán?

Problema 2

En una carrera de relevos los corredores de dos equipos esperan a recibir el testigo para recorrer los 200 metros que les separan de la meta. Uno de ellos sale primero con una velocidad de 2 m/s. El otro, que recibe el testigo 15 segundos después, empieza a correr con una velocidad de 2,5 m/s. El corredor que salió más tarde gana la carrera, pero, ¿qué distancia recorrió hasta alcanza a su rival?

Problemas de dos móviles con orígenes diferentes

Problema 3

Dos ciclistas quieren ir a la misma ciudad por el mismo camino. Los dos salen a la vez, el primero de un punto situado a 30 km de la meta con una velocidad de 12 km/h y el segundo sale desde un punto ubicado a 40 km y lleva una velocidad de 18 km/h. Han quedado que cuando se encuentren pararán a saludarse, ¿cuántos kilómetros les faltarán para llegar a su destino?

Problema 4

Dos amigos están jugando a pillar en el parque. Cuando empieza el juego están separados 30 metros. El que ha de pillar corre con velocidad de 5 km/h y el que está delante corre a 4 km/h. ¿Qué distancia habrá recorrido el que ha de pillar al otro cuando lo alcance?

Problemas de dos móviles con orígenes y tiempos de salida diferentes

Problema 5

Encima de una mesa hay dos caracoles. Ponemos una hoja de lechuga a 20 cm del primer caracol y a 25 cm del segundo. El caracol más cercano la ve enseguida y va hacia ella a una velocidad de 1,5 cm por minuto, el que estaba más lejos, que estaba despistado, la ve 3 minutos después y empieza a moverse a un ritmo de 3,5 cm por minuto para intentar llegar antes. ¿Qué distancia habrá recorrido el caracol que salió más tarde cuando alcance al otro?

Problema 6

Dos skaters han quedado en encontrarse de camino a un parque. El primero vive a 2 km del parque y sale de casa a las 12:00 con una velocidad de 1,5 m/s. La casa del segundo está a 1 km del parque y sale de su casa a las 12:10 con una velocidad de 1 m/s. ¿Cuántos metros caminó el que salió primero hasta encontrar a su amigo?

ANEXO II: PROTOCOLO DE CALIFICACIÓN DE LOS PROBLEMAS

La puntuación máxima para cada problema es de 1 punto, repartido en los apartados que se describen a continuación. Las puntuaciones de cada apartado son acumulables.

1. Elabora un diagrama compatible con los datos y la información del enunciado que sirva como base para iniciar la resolución del problema

• Presente: + 0,1
• Ausente: 0

2. Plantea adecuadamente las ecuaciones x = f(t) respetando los límites del problema, en especial las referentes a las condiciones iniciales de posición y tiempo.

• Por cada ecuación correcta: + 0,1 (0,2 máximo)
• Por cada ecuación incorrecta o incompleta: 0

3. Realiza mecanismos de resolución de las ecuaciones, en este caso la igualación o la sustitución.

• Si iguala o sustituye las ecuaciones correctamente: + 0,2

4. Despeja correctamente t a partir de las ecuaciones

• Sí: + 0,2
• No: 0

5. Una vez obtenido t, sustituye correctamente para obtener x

• Si: + 0,1
• No: 0

6. Presenta claramente el resultado a la cuestión planteada

•  Alcanza el resultado correcto, respondiendo a la cuestión planteada: + 0,2
•  No alcanza el resultado correcto: 0

Nota 1: En caso de que las ecuaciones no estén planteadas correctamente pero el alumno demuestre que conoce el proceso de resolución del sistema de ecuaciones (igualación o sustitución) la puntuación total será 0,2 (0,3 si incluye un diagrama correcto al inicio).

Nota 2: Un problema resuelto por el método de tanteo no se considera válido aunque el alumno llegue a la respuesta correcta. Un alumno que, empleando este método alcance el resultado correcto, obtendrá una puntuación total de 0,2 (0,3 si la respuesta incluye un diagrama correcto).

 

ANEXO II: PROTOCOLO DE CALIFICACIÓN DE LOS PROBLEMAS

Modelo 1 (Señalización real o directa)

Verás a continuación dos problemas. Debes tratar de resolverlos indicando los pasos que realizas. Resuelve cada problema en una hoja diferente poniendo en la esquina superior derecha tu nombre. Puedes usar la calculadora si lo necesitas. Muchas gracias por tu colaboración.

Problema 1

Dos coches salen del mismo punto para realizar un trayecto por una carretera recta. El primero sale a las 12:00 h con una velocidad de 100 km/h y el segundo sale a las 12:30 h con una velocidad de 120 km/h.¿A qué distancia del punto de origen se encontrarán?

Problema 2

Dos ciclistas quieren ir a la misma ciudad por el mismo camino. Los dos salen a la vez, el primero de un punto situado a 30 km de la meta con una velocidad de 12 km/h y el segundo sale desde un punto a 40 km de la meta y lleva una velocidad de 18 km/h. Han quedado que cuando se encuentren pararán a saludarse, ¿cuántos kilómetros les faltarán para llegar a su destino?

Modelo 2 (Señalización inversa)

Verás a continuación dos problemas. Debes tratar de resolverlos indicando los pasos que realizas. Resuelve cada problema en una hoja diferente poniendo en la esquina superior derecha tu nombre. Puedes usar la calculadora si lo necesitas. Muchas gracias por tu colaboración.

Problema 1

Dos ciclistas quieren ir a la misma ciudad por el mismo camino. Los dos salen a la vez, el primero de un punto situado a 30 km de la meta con una velocidad de 12 km/h y el segundo sale desde un punto a 40 km de la meta y lleva una velocidad de 18 km/h. Han quedado que cuando se encuentren pararán a saludarse, ¿cuántos kilómetros les faltarán para llegar a su destino?

Problema 2

Dos coches salen del mismo punto para realizar un trayecto por una carretera recta. El primero sale a las 12:00 h con una velocidad de 100 km/h y el segundo sale a las 12:30 h con una velocidad de 120 km/h.¿A qué distancia del punto de origen se encontrarán?